
Are you searching for cross product problems for better understanding? Wait! you are in the right place. In this article, we are going to explain the problems of the cross product.
Mathematics! The monster in every kids’ dream. The ‘yucky’ part of doing homework every day after school. The ‘ew’ is heard by the parents whenever they ask how their kids’ Maths class was. Indeed, these imply the distaste of it and so definitely, not everyone’s cup of tea.
To add to this comes the big bad guy – ‘Algebra’ to instill fear in the young kids. The stories they have heard from their older siblings: ‘Once Algebra starts for you, you are done for.’ ‘You don’t know basic multiplication. What will you do when Algebra starts, God, knows!’
Everyone has heard these dialogues at least once in their life during their school years, and the fear was indeed genuine. And true to its rumor, it did make us suffer in more ways than one.
But, the difference between now and then is that, in the world of advanced technology and the availability of an unlimited variety of audio-visual aids, we can now use a more practical approach for understanding.
To understand Algebra, a three-dimensional imagination (since space is three-dimensional) is a must, and thus it is difficult to explain on paper that it is two-dimensional. Hence, the difficulty was back then and the technology makes it easy now. For instance, We made a tool called Cross Product Calculator which is a free online calculator for finding the cross product of two vectors.
Now, let us begin from the basics of cross-product and slowly understand the problems of cross product.
What is a CROSS PRODUCT?
The vector multiplication or the product of two vectors (say A and B) is known as the cross product or vector products (denoted by A X B).
The result between the two vectors is referred to as ‘c,’ which is perpendicular to both the vectors, a and b, Where θ is the angle between two vectors.
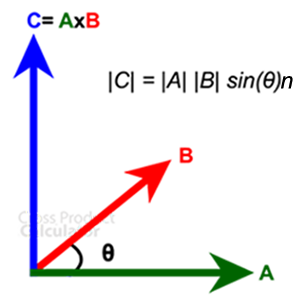
CROSS PRODUCT FORMULA
a ⨯ b = |a| |b| sin (θ) n
- | a | and | b | ➜ Length of two vectors.
- θ ➜ Angle between the two vectors a and b.
- n ➜ unit vector perpendicular to both vectors a and b.
CROSS PRODUCT PROBLEMS
Problem 1 :
Two vectors are given as:
![]()
Find the cross product between the two vectors.
Solution :
Given –
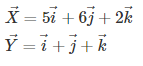
The representation of the above two vectors using cross product matrix method is given by –
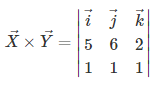
On expansion,
![]()
The final answer obtained is,
![]()
Problem 2 :
Two vectors are given as:
![]()
Find the cross product between the two vectors.
Solution :
Given Vectors
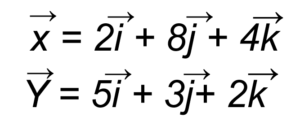
The representation of the above two vectors using cross product matrix method is given by –
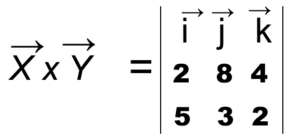
On expansion,
![]()
The final answer obtained is,
![]()
Problem 3 :
Vector a has magnitude 7 and vector b has magnitude 2, the angle between a and b is 45° and n is the unit vector at right angles to both a and b
What is a × b ?
Solution :
we knew that formula of the cross product is a ⨯ b = |a| |b| sin (θ) n
|a| = 7, |b| = 2 and θ = 45°
Hence, a × b = 7× 2 × sin(45°) × n = 12 × 0.8 × n = 9.6n
Problem 4 :
Calculate the area of the parallelogram spanned by the vectors a=(2,1) and b=(4,3)
Solution :
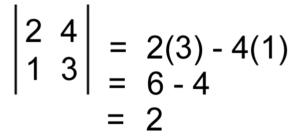
Hence, the Area of a parallelogram spanned by the vectors a=(2,1) and b=(4,3) is 2
