Solution :
| i | j | k |
|---|---|---|
| x1 | y1 | z1 |
| x2 | y2 | z2 |
Cross Product Calculator ( Vector )
Cross Product Calculator
Are you in search of an online calculator that makes quick calculations and displays the cross product results in fraction of seconds? Then Our free calculator exactly helps you in finding the cross product between 2 vectors.
VECTOR X
VECTOR Y
| y1 | z1 |
| y2 | z2 |
| x1 | z1 |
| x2 | z2 |
| x1 | y1 |
| x2 | y2 |
on expansion x * y = i(y1.z2 – z1.y2) -j(x1.z2 – z1.x2) +k(x1.y2 – y1.x2)
The vector cross product calculator is pretty simple to use, Follow the steps below to find out the cross product:
Check out this article for a better understanding of how to use the calculator.
-
- Step 2 : Click on the “Get Calculation” button to get the value of cross product.
- Step 3 : Finally, you will get the value of cross product between two vectors along with detailed step-by-step solution.
Check out this article for a better understanding of how to use the calculator.
What is a CROSS PRODUCT?
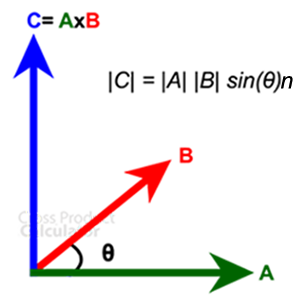
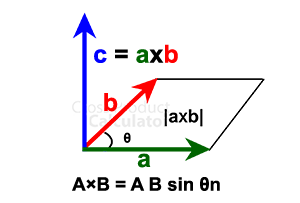
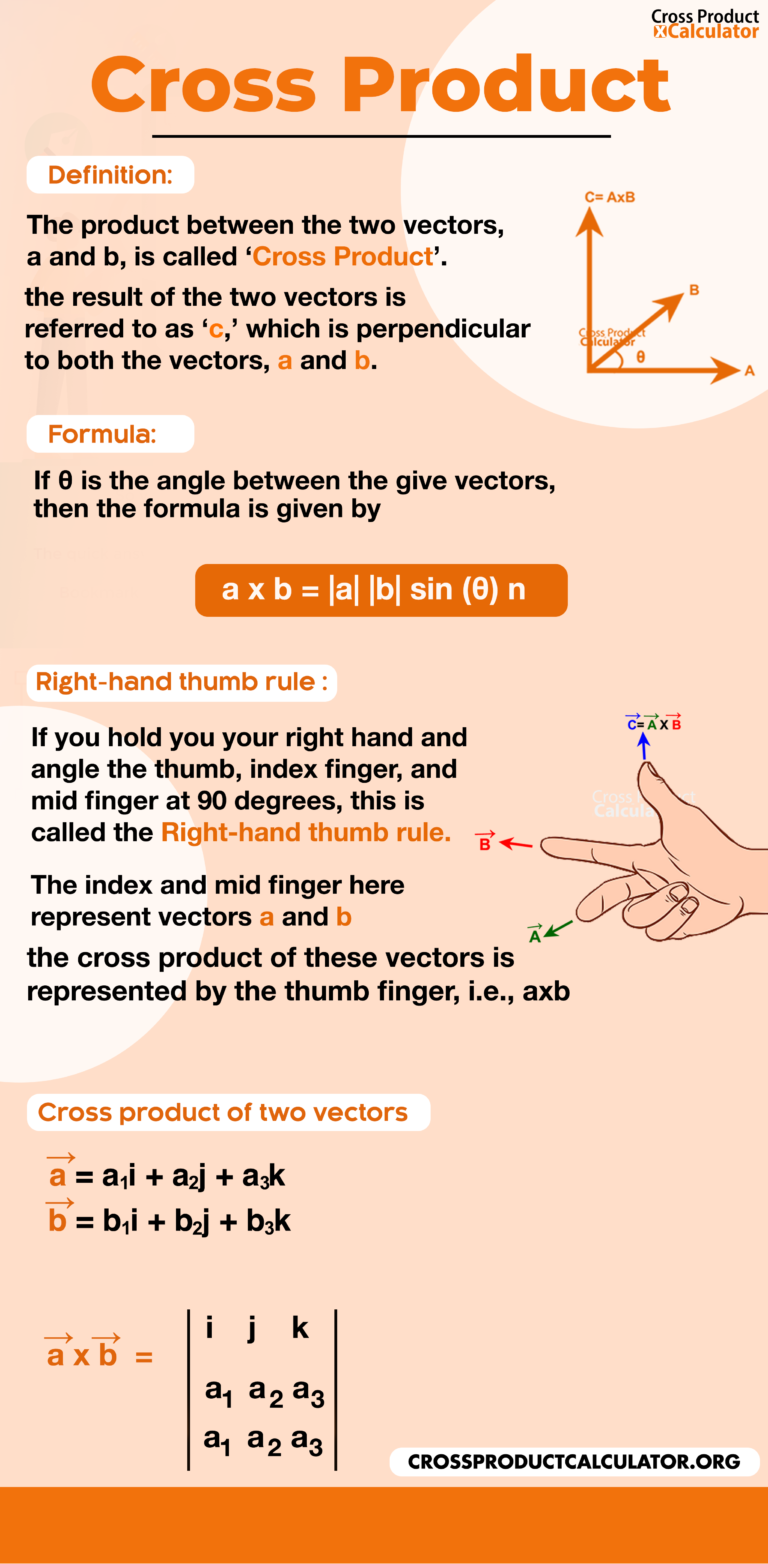
The product between the two vectors, a and b, is called ‘Cross Product.’It can only be expressed in three-dimensional space and not two-dimensional. It is represented by ‘a ⨯ b’ (said a cross b).
The result of the two vectors is referred to as ‘c,’ which is perpendicular to both the vectors, a and b, Where θ is the angle between two vectors. Its direction is given by the right-handed rule and the magnitude is given by the area of a parallelogram.
CROSS PRODUCT FORMULA
a ⨯ b = |a| |b| sin (θ) n
If vectors a and b are parallel, then their cross product is zero.
The direction of the vector c can simply be known by the right-hand thumb rule, where-
The forefinger should be in the direction of a.
The middle finger should be in the direction of b.
The cross product formula is a bit more complex than the usual formulae. A bit more concentration and an open, clear mind are required. Focusing on the basics will help you understand the concept better.
The direction of the vector c can simply be known by the right-hand thumb rule, where-
The forefinger should be in the direction of a.
The middle finger should be in the direction of b.
The cross product formula is a bit more complex than the usual formulae. A bit more concentration and an open, clear mind are required. Focusing on the basics will help you understand the concept better.
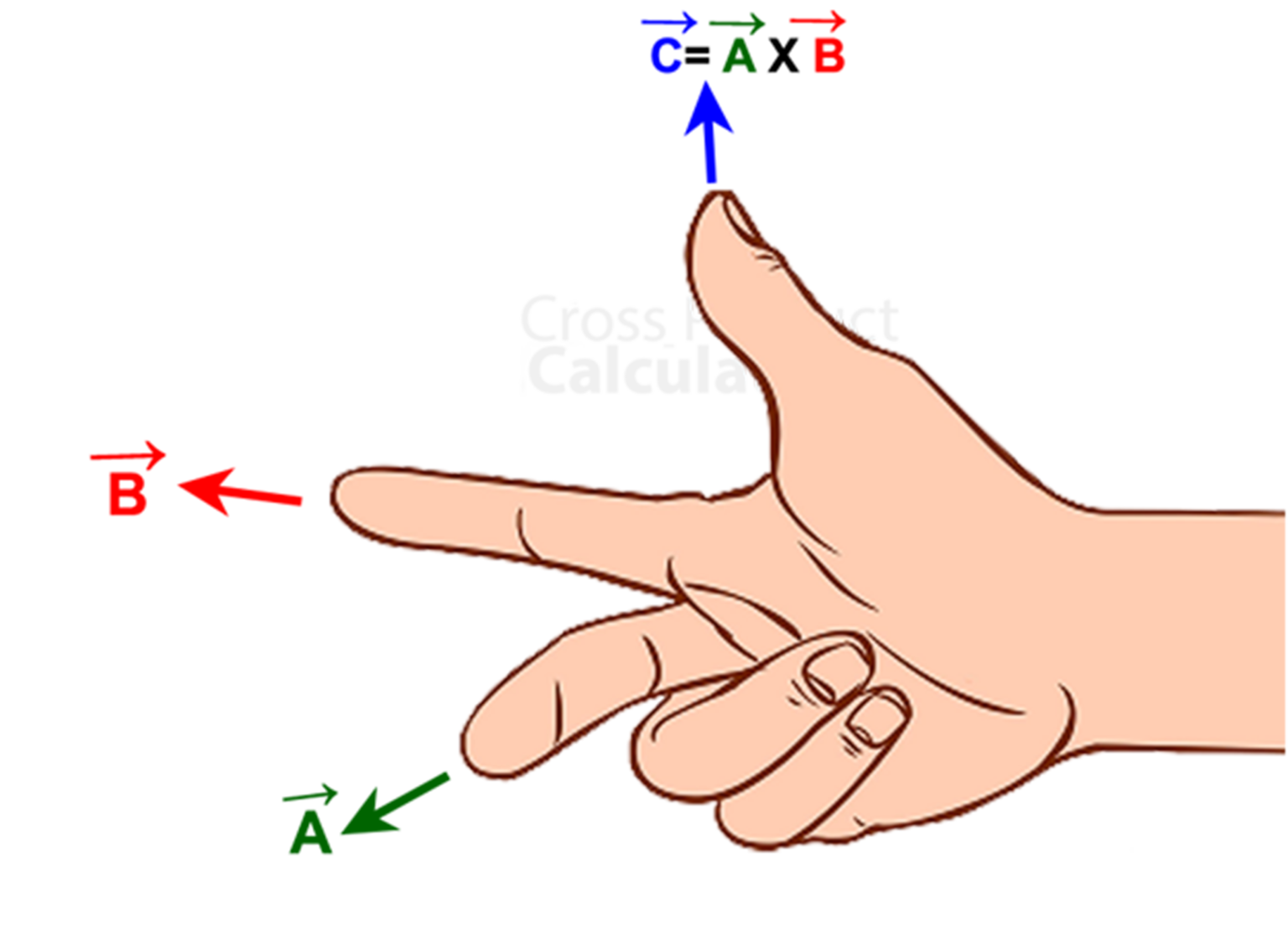
We can find the direction of the unit vector by taking into account the right hand rule for cross product. To decide the right cross-product, we have a right-hand rule.
For making use of this rule, you hold your right-hand up, then lift your index finger and en route towards the first vector, and now point your middle finger in the direction of the second vector. While doing this, the thumb of your right hand will show the direction of the unit vector.
Solved Example of Cross Product
Two vectors are given as:
Find the cross product.
Solution :
Given –
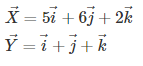
The representation of the above two vectors using cross product matrix method is given by –
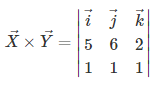
On expansion,
The final answer obtained is,
Check here for more cross product problems.
What is a Vector?
It is a measurement of one point in space relative to another point in space. It has two components – magnitude and direction. Vectors are helpful to know the position, displacement, velocity, and acceleration of an object.
Magnitude is the value of the length of the vector. It is denoted by ‘||a||.’
Direction is the angle of rotation of the vector with respect to east, west, north, and south. It is denoted by ‘→’, which has two ends: the tail and the head. The direction of the arrow depends on the vector, i.e., if it’s forwards, backwards, upwards, or downwards (usually just forwards and backwards).
Types of Vectors
There are two types of vectors :
1. Parallel Vectors
2. Perpendicular Vectors
1. Parallel Vectors
2. Perpendicular Vectors
1. Parallel Vectors :
Two vectors, a and b, are parallel when their scalar multiples are zero.
a = kb, where ‘k’ is a constant which means, it is not equal to zero.
Let a = (ax , ay) and b = (bx , by) a and b are parallel, if and only if
a = kb (ax , ay) = k (bx , by) = (kax , kby)
Two vectors, a and b, are parallel when their scalar multiples are zero.
a = kb, where ‘k’ is a constant which means, it is not equal to zero.
Let a = (ax , ay) and b = (bx , by) a and b are parallel, if and only if
a = kb (ax , ay) = k (bx , by) = (kax , kby)
2. Perpendicular Vectors:
Two vectors, a and b, are perpendicular when their scalar products are zero.
a = kb, where ‘k’ is a constant which means, it is not equal to zero.
Let a = (ax , ay) and b = (bx , by) a and b are perpendicular, if and only if
a.b = 0 (ax , ay) . (bx , by) = ax bx + ay by
Two vectors, a and b, are perpendicular when their scalar products are zero.
a = kb, where ‘k’ is a constant which means, it is not equal to zero.
Let a = (ax , ay) and b = (bx , by) a and b are perpendicular, if and only if
a.b = 0 (ax , ay) . (bx , by) = ax bx + ay by
Types of Products
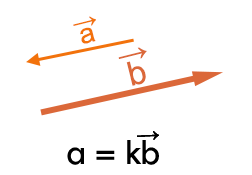
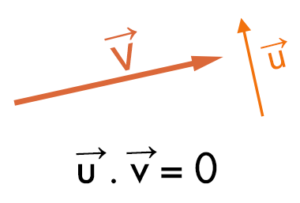
The need to know the product of two vectors is to find which one is perpendicular to both vectors.
There are two ways to calculate the product of two vectors :
- 1. Dot Product
- 2. Cross Product
- 1. Dot Product (also called scalar product):
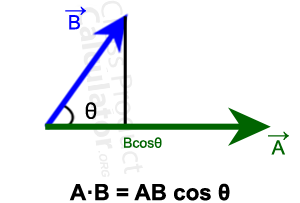
It gives the level at which how much the two vectors point in the same direction.
It is represented by a . b = ||a|| ||b|| cos (θ)
Where, a and b are the two vectors
and θ is the angle between the two vectors, a and b.
- 2. Cross Product (also called vector product) :
It is represented by a ⨯ b = ||a|| ||b||sin (θ)n
Where, a and b are the two vectors
and θ is the angle between the two vectors, a and b.
- 1. A number is given by the dot product, while a vector is provided by the cross product.
- 2. In any number of dimensions, dot products can be used, but the cross product is only for three dimensions.
- 3. The result of a dot product is a scalar quantity, but the result of a cross product is a vector quantity.
4.The similarity in the direction of two vectors is measured by dot product, whereas the difference in the direction of two vectors is measured by cross product.Also check this : Difference between cross product and dot product
COORDINATE NOTATION: STANDARD METHOD
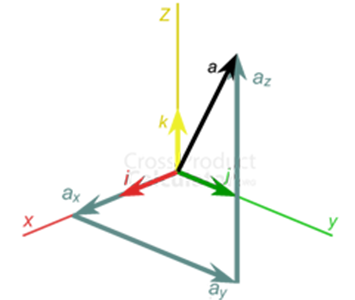
Consider two vectors A and B where,
A = ai + bj + ck
B = xi + yj + zk
Here, i is unit vector in the x-axis
j is unit vector in the y-axis
K is unit vector in the z-axis
We know that the relationships between i,j, and k, which are called Equalities, are as follows –
i × j = k and j × i = –k
j × k = i and k × j = –i
k × i = j and i × k = –j
Note: Due to anti-commutative property (see below) and no linear independence (no linear combination exists), we can say that –
i × i = j × j = k × k = 0
So,
A × B = (ai + bj + ck) × (xi + yj + zk)
= ax(i × i) + ay(i × j) + az(i × k) + bx(j × i) + by(j × j) + bz(j × k) + cx(k × i) + cy(k × j) + cz(k × k)
By using the above given Equalities,
A × B = ax(0) + ay(k) + az(-j) + bx(-k) + by(0) + bz(i) + cx(j) + cy(-i) + cz(0)
= (bz – cy)i + (cx – az)j + (ay – bx)k
CROSS PRODUCT MATRIX: AN ALTERNATIVE METHOD
Other than the standard method, another alternative applicable for application is the ‘cross product matrix’ method.
The difference between the standard and cross product matrix methods is that the determinants are not used in the former but the latter.
Consider two vectors A and B where,
A = ai + bj + ck
B = xi + yj + zk
Here, i is unit vector in the x-axis
j is unit vector in the y-axis
K is unit vector in the z-axis
The cross product matrix method is represented by –
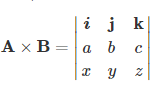
Where,
A × B = (bz – cy)i – (az – cx)j + (ay – bx)k
= (bz – cy)i + (cx – az)j + (ay – bx)k
OR
These are also called – ‘Formal Determinants’ and given as below –
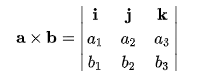
Applying Sarur’s Rule of Cofactor Expansion,
The expansion results in –
Properties of Cross product
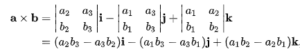
Properties play a big part in finding out cross-products of the various given vectors that layout guidelines in certain conditions. They bind the solutions of cross-products obtained. There are four properties, out of which the top two are most important. They are –
- 1. Anti-commutative Property
This property primarily exhibits negative signs.
Represented as –
The anti-commutativity takes part in the coordinate notation method, and so the equalities i, j and k become -i, -j, and -k, respectively.
2. Distributive Property
It shows us how to find the solution to expressions like a (b + c). It is also called the ‘Distributive Law of Multiplication and Division.’
Represented as –
Usually, while solving an expression of the above pattern, we solve the equation in the parentheses first. Still, when it comes to distributive property, we must first multiply the numbers outside the parentheses with the numbers inside it in the proper order.
Example:
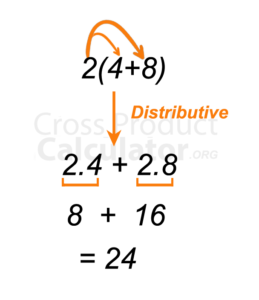
In the above example, we observe that 2 is multiplied by 4 followed by 8, and then their resultant is added, and we get the answer 24.
If we use the standard method mentioned earlier, we would still get the answer as 24. Then why are we using the distributive property? When it comes to vectors, often instead of numbers, variables are present as coefficients. When variables are present, we have to use the distributive property and not the standard method; otherwise, we will get wrong answers.
- 3. Jacobi Property
It is named after the German Mathematician, Carl Gustav Jakob Jacobi.
Represented as –
This property keeps in check the order in which expressions are supposed to be calculated and the position of parentheses in a multiple order expression. This is necessary to maintain uniformity in solving similar types of expressions all over the world.
It has various forms depending upon the subject of usage.
- 4. Zero Vector Property
Represented as –
It has three definitive sub-properties. They are –
(i) An additive identity, meaning a + 0 = a.
(ii) Zero multiplied with any vector in space results in this property, meaning 0 (a) = 0.
(iii) Right angles (orthogonal) to every vector in space, meaning a . 0 = 0.
Frequently asked questions!
What is a Vector Cross Product Calculator?
It is a vector multiplication calculator for finding the cross product between two vectors.
The calculator is pretty simple to use, whether you need it for academic or personal use, you can simply key in the digits and press enter to find the answer. Our calculator also provides a detailed step-by-step solution along with a direct answer.
How to calculate 2D and 3D Vectors?
There are two types of calculators that are used respectively for 2D or 3D vectors i.e., based on the number of vectors’ dimensions which could be two or three. For example, if a user is using vectors with only two dimensions, then a Cross product calculator 2×2 can be used for 2 vectors. Here, the user fills in only the ‘i’ and ‘j’ fields, hence leaving the third field ‘k’ blank. If the user uses the calculator for a 3D vector as in the case of a Cross product calculator 3×3, then the user has to enter all the fields. Here, there are values entered for all the three dimensions in the respective i, j, and k fields which are multiplied together and then added up to give the total resultant.
How does this calculator work?
Without the aid of a vector cross product calculator, it is hard to calculate the cross product of two vectors. Academically or otherwise, you may already know the formula for the cross product of two vectors. Fortunately, this calculator is such a tool that helps you understand the formula. To add on, there is quite a list of practical tricks such as the right-hand rule, wherein you can master the trick of how to do the cross product of two or three vectors.