
Calculus is a complex part of Math. Even genius minds need to understand its core fundamentals to grasp this branch of arithmetic.
To calculate the position of anything that exists and has dimensions, cross product and dot product are used. These consider the coordinates of the number of dimensions, their magnitudes, and directions, finally giving the exact position.
This is done to define a particle’s address in the unlimited space around us. Let’s take, for instance, an electron.
It is so minute that you cannot calculate its location using centimeters or even millimeters. Also, it is inevitable to figure out the location without considering different dimensions because of its tininess.
Hence, Dot Product is what you need to get a pinpoint site of a nanoscopic particle.
What is a DOT PRODUCT?
With various directions and magnitudes, you need to consider when calculating the position of any particle/object in space (both two and three dimensions). Hence, these have been divided into two calculation types that will bifurcate separate calculations for easy understanding.
There are two lanes to go down; the first uses the cross product, whose product is again vector in nature. The second is using dot product, whose product is not a vector but a scalar.
A scalar value is a number that gives a definite value, unlike a vector product that is not definite and is instead a variable. Although this difference is present, it does have the magnitude and direction of its product.
What is the Dot Product of Two Vectors?
Since its a product, it will involve two different values. So these are multiplied to get the final product.
Dot Product determines the similarity between the two selected values for calculation and not the difference between them like the cross product. Therefore, it can be both positive and negative in its value.
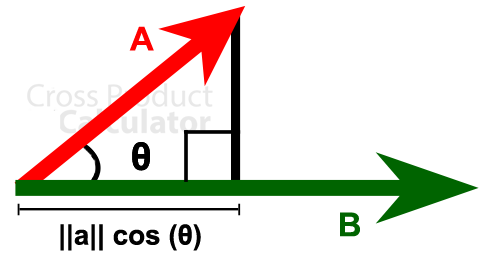
Let us consider two different vectors, a and b. The product between these two vectors, a and b, is called a ‘Dot Product.’
a . b = ||a|| ||b|| cos (θ)
- a and b are the two vectors.
- θ is the angle between the two vectors a and b (ranges between 0° to 180°).
The angle between the two vectors is significant. This angle decides whether the dot product will be positive or negative (or bigger or smaller in value).
For example, let us consider two cases,
Case 1:
Let the θ value be ‘0’, meaning both the vectors overlap each other without the slightest discrepancy. They are perfectly aligned, pointing in the same direction.
So, the representation will become – a . b = ||a|| ||b|| cos (0)
Cos (0) = 1
Therefore, whatever the value of a and b may be, now that the angle value is 1, the product between them will give the dot product a greater than 1.
The greater the dot product value, the similar will be the value of the direction of the particle/object in question.
Case 2:
Let the θ value be ‘1’, meaning both the vectors are perpendicular to each other precisely at right-angled positions. Thus, in the directional sense, if one points north, the other is pointing at east.
So, the representation will become – a . b = ||a|| ||b|| cos (90)
Cos (90) = 0
Therefore, whatever the value of a and b may be, now that the angle value is 0, the product between them will be obviously 0.
Case 3:
How can a dot product be negative?
If the angle between them is cos (180), i.e., both the vectors are connected by one of their ends, pointing in opposite directions, then the value will indeed be 1, but with a negative sign before it. And so, the negative existence of dot product can be justified.
Dot Product Formula
There are two formulae, depending on the type of mode of calculation. The value will remain the same for both types, except for representation.
Algebraic Expression
A concise expression has been formulated for easy calculation. And that is –
Where, a is first vector
b is second vector
Σ is summation; it is the total of all the dimensional dot product values
n is the dimension number (n=1,2,3,……..)
Here, a1, a2, a3………an are all the values only concerning vector a, but in different dimensions, like
a1 is for x-axis,
a2 is for y-axis
a3 is for z-axis
And so on.
The same is the case for vector b.
Values of both a and b vectors are used to get the final product.
Geometric Expression
This expression, unlike the Algebraic Expression, involves the angle. Hence, θ holds much importance here.
The Geometric Expression is – a . b = ||a|| ||b|| cos (θ)
Where, a and b are the two vectors.
θ is the angle between the two vectors, a and b.
Here, θ are mostly 0°,30°, 45°, and 90°, and their respective values are 1, √3/2, √1, and 1/2.
How to do Dot product?
To do Dot Product, there are two methods in Algebraic Expression. However, there can be more than two methods if there are more than two dimensions: three or four and so forth.
Two-Dimensional Dot Product :
The Algebraic Expression for a two-dimensional representation is –
a · b = ax × bx + ay × by
Where, a and b are the two vectors of which the dot product is to be calculated.
ax is the x-axis
ay is the y-axis
are the values of the vector a.
bx is the x-axis
by is the y-axis
are all the values of the vector b.
On solving the above expression, you will get the dot product of a two-dimensional particle/object.
Three-Dimensional Dot Product :
The Algebraic Expression for a three-dimensional representation is almost the same; save the addition of another dimension after x and y, i.e., z.
a · b = ax × bx + ay × by + az × bz
Where, a and b are the two vectors of which the dot product is to be calculated.
ax is the x-axis
ay is the y-axis
az is the z-axis
are all the values of the vector a.
bx is the x-axis
by is the y-axis
bz is the z-axis
are all the values of the vector b.
On solving the above expression, you will get the dot product of a three-dimensional particle/object.
Dot product Examples
Algebraic Expression
Two-Dimensional Dot Product
E.g. The coordinates for the x-axis and y-axis for the vectors a and b are given as (-4,8) and (3,6)
Solution: Substitute the coordinate values in the formula for the two-dimensional dot product.
Formula : a · b = ax × bx + ay × by
Substituting, we get –
a . b = (-6 × 5) + (8 × 12)
On solving, we get –
a . b = (-30) + (96)
a . b = -30 + 96
a . b = 66
Therefore, the dot product of vectors a and b is 66.
Three-Dimensional Dot Product
E.g. The coordinates for the x-axis, y-axis, and z-axis for the vectors a and b are given as – (4,8,10) and (9,2,7)
Solution: Substitute the coordinate values in the formula for the two-dimensional dot product.
Formula – a · b = ax × bx + ay × by + az × bz
Substituting, we get –
a . b = (4 × 9) + (8 × 2) + (10 × 7)
On solving, we get –
a . b = (36) + (16) + (70)
a . b = 36 + 16 + 70
a . b = 122
Therefore, the dot product of vectors a and b is 122.
Geometric Expression
E.g. For vectors a and b, the values are 10 and 13. The value of θ is 59.5°
Solution: Substitute the values in the formula.
Formula – a . b = ||a|| ||b|| cos (θ)
Substituting, we get –
a . b = ||10|| ||13|| cos (59.5)
On solving, we get –
a . b = ||10|| ||13|| 0.5075
a . b = 10 × 13 × 0.5075
a . b = 65.98 which is almost 66
Therefore, the dot product of vectors a and b is 66. Now go back and compare the answer we got using Algebraic Expression.
You will observe that both the answers are ‘66’ irrespective of the method used. Hence it is proved that both the methods result in the same.
Conclusion
On a moderate level, the dot product is used in math and physics. On a larger scale, the dot product is used to study space, its components, what type of particles and objects are found, their dimensions, etc.
Therefore, the dot product is essential and significant for discovering the still hidden secrets of space.

