
When studying technical subjects like physics or mathematics, one of the most common questions we find ourselves asking is, “Why should we study this and how is it going to help us in the future?”
I’d love to answer this question for you. The truth is, every aspect of the subjects you learn have some or the other application in your real-life, be it skill wise, content wise, or simply as a matter of gaining an attribute.
A common topic that every student would despise getting into, is vector algebra. Although it may look tricky at face value, in this article we’re going to cover the difference between cross product and dot product. Before we step into it, let’s understand what vector algebra is and how its study can be beneficial.
Vector algebra, as its name suggests, deals with vectors. Most quantities are either scalars or vectors. Scalars only have magnitude whereas vectors have both magnitude and direction.
Now that we’ve understood the importance of vector algebra, let’s get into dot product and cross product specifically.
Difference between cross product and dot product
1. The main attribute that separates both operations by definition is that a dot product is the product of the magnitude of vectors and the cosine of the angles between them whereas a cross product is the product of magnitude of vectors and the sine of the angles between them.
2. While this is the dictionary definition of what both operations mean, there’s one major characteristic that segregates them both. That difference can be noted in terms of vector algebra. The result of a dot product is a scalar quantity with magnitude as its whole, however, the result of a cross product is a vector quantity with both magnitude and direction.
These are the two main differences you must take note of to understand the concepts at face value.
Let’s take a mathematical approach to get familiar with it a bit more:
A dot product is represented the following way:
a . b = ||a|| ||b|| cos (θ)
Here A and B are vectors and is the angle between both vectors.
A Cross product is represented the following way:
a . b = ||a|| ||b|| sin (θ) n
Here A and B are vectors and is the angle between them. N is the unit vector perpendicular to the plane that A and B are a part of.
DOT PRODUCT VS CROSS PRODUCT (Tabular Form)
This will give you a summed up idea of the differences between both operations, in simpler words.
| Factors of Comparison | Dot Product | Cross Product |
|---|---|---|
| General Definition | Product of magnitude of vectors and cos of the angle between them. | Product of magnitude of vectors and sine of the angle between them. |
| Mathematical Formula | In terms of vectors A and B A · Β = |A| |B| cos θ | In terms of vectors A and B A × Β = |A| |B| sin θ n |
| Result | The final product is a scalar quantity. | The final product is a vector quantity |
| Result With further explanation | Scalar: Only Magnitude. | Vector: Both magnitude and direction. |
| Property 1: Commutativity | Follows a commutative law: A.B=B.A | Does not follow a commutative law: AxB is not equal to BxA |
| Property 2: Orthogonality of vectors | The dot product is zero when the vectors are orthogonal, as in the angle is equal to 90 degrees. What can also be said is the following: If the vectors are perpendicular to each other, their dot result is 0. As in, A.B=0 | Whereas, the cross product is maximum when the vectors are orthogonal, as in the angle is equal to 90 degrees. What can also be said is the following: If the vectors are parallel to each other, their cross result is 0. As in, AxB=0 |
| Property 3: Distribution | Dot products distribute over addition | Cross products also distribute over addition |
| Property 4: Scalar Multiplication Law | Scalar Multiplication Law is followed by Dot Products | Scalar Multiplication Law is also followed by Cross Products |
What does this mean theoretically?
Dot Product :
Due to having only magnitude and no direction, both vectors in a dot product operation are aligned the same way. The cosine of the angle between these vectors is taken. The product comes out to be scalar. It is also known as inner product or projection product. The product has 4 distinct properties known as commutative, distributive, orthogonal, or one that follows the scalar multiplication law.
The product has 4 distinct properties known as commutative, distributive, orthogonal, or one that follows the scalar multiplication law.
Applications of Dot Product:
The operation is used to define the length between two points on a plane, with known coordinates.
Cross Product :
Due to having both magnitude and direction, the magnitude of the vectors is taken along with the sine of the angle between them. As a result, the product comes out to be a vector quantity. It’s important to note that the final result of the cross product operation must be perpendicular to both vectors, or in other words, the plane that both vectors lie on.
Thus, the right-hand thumb rule can be used to find the direction. In that case, the two fingers represent the vectors and the thumb determines the product. A cross product is also known as directed area product.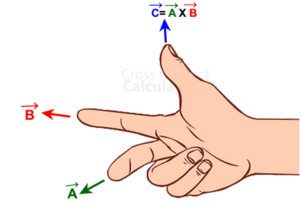
Just like the dot product, cross product also has 4 distinct properties. It is non-commutative, distributive, orthogonal, and compatible with the scalar multiplication law.
Applications of Cross Product:
Mainly applied in computational geometry to find or define the distance between two skew lines. Cross product can also be used to suggest if two vectors are coplanar or not.

Conclusion:
Vector algebra that covers dot and cross products is a beneficial topic for aspiring physicians and mathematicians as it gives an insight into basic geometry and trigonometry that can be applied in real-world situations. In mathematics, addition, subtraction, and multiplication on vectors can be performed to understand the nature of a plan or trajectory, whereas in physics, vectors like distance, displacement, velocity, and acceleration are used to understand more extreme subjects.
Euclidean’s vectors have been used for several hundred years now, making a lot of contributions to the math and physics sectors. They were analyzed, evaluated, and reworked on after several scientists and mathematicians developed the concept, making alterations and innovations as new information would come into the picture.
Once understood, vectors can be an interesting topic to further your study on, and also apply in your life. We hope this article on dot and cross products helped you to understand the basic differences in terms of formula, properties, and applications!
