Cross Product Calculator ( Vector )

Uncategorized

Right Hand Rule For Cross Product

Cross products have various applications that are very important in the real world.
In this article, you will learn to use the right hand rule for cross product through some examples.

Cross Product

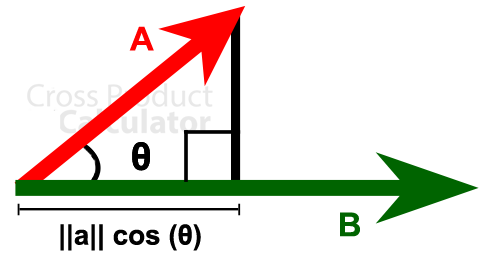
If A and B are taken as two independent vectors, then the cross product of these two vectors (AB) will be perpendicular to both the vectors, and it will be normal to the plane having both vectors. It can be represented as-.
a . b = ||a|| ||b|| cos (θ)

The critical thing to remember is that the result is a vector and NOT a scalar value. This is why it is known as vector product. For the definition easy to remember, we generally use determinants to calculate cross products and we made a cross product calculator that helps you in finding the cross product of two vectors.

To calculate the position between vectors we also use dot product and the difference between cross product and dot product is the result of cross product will be vector quantity while the result of dot product will be scalar quantity.

Right Hand Rule For Cross Product

In maths and physics, the right hand rule is a standard illustration for assimilating notation conventions for vectors in 3-D. It was for the first time introduced by John Ambrose Flemming in the late 19th century.
As I already said, there are two noticeable solutions for vectors at right angles to each other. So, while using this idea, one must remove the ambiguity of which solution is meant.

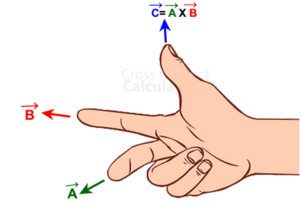
One type of right hand rule is used while performing an ordered operation on two vectors, let it be “a” and “b”. And the result of this is a vector “c” that is perpendicular to each “a” and “b”.

So to impose the right hand rule, you should follow the below-given instruction to choose one of the two directions.

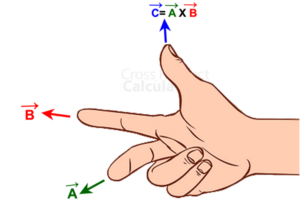
Right hand thumb rule
  • Hold up your right hand. Taking the left hand won’t work.
  • Arrange your thumb, index and middle finger at right angles to each other in a way that your index finger should be pointed straight.
  • The middle finger should be in the direction of vector product . Here, the thumb will represent vector “a”, and the index finger will represent vector “b”.
  • Nevertheless, interchangeable finger assignments are also possible.

Another form of right-hand rule is taken into account when a vector is assigned for the rotation of the body or a magnetic field. Conversely, if a vector specifies any rotation and you have to find how the cycle occurs. Then, this second form of right hand rule, also called the right-hand grip rule, comes into use in such cases.

  • Curl fingers of your right hand (hence the name) in a way that follows the rotation of vectors “a” and “b”. Then your thumb will point towards the vector product that is “c”.

This method is taken into consideration when you have to find the direction of the torque vector. When you grip the imaginary axis of the rotation due to a rotational force, your fingers will show the guide of the force, and your extended thumb will point in the direction of the torque vector.

Right Hand Rule For Cross Product

Its highly useful to know the cross product between the distinct unit vectors , and .
For instance, consider
×
Here, because the vectors are perpendicular or orthogonal, their magnitude will be-
= = (1) (1) = 1
Now because the unit vectors have magnitude 1. The cross product has to be straight-up or perpendicular to and
This suggests that it must point along the z-axis. And because it has length 1, it can be either or .
How to decide which one it is? Well, it’s arbitrary. We can choose any of the two options, and it will work the same way in mathematics.
But, of course, it will be constructive if we all agree on the same result.
We have decided this, and this particular choice is called a right-handed coordinate system.
So, if you have to choose a coordinate system for a problem, then make it a right-hand coordinate system or else there will be a chance of getting incorrect answers.

Some Applications of Right Hand Rule

  • It is used to ascertain the direction of the cross or vector products.
  • To find the torque and force that causes it.
  • Also, it can be used to find the position of the application of the force that’s causing it.
  • It can be helpful in magnetic fields to determine the position of the electric current
  • To find the magnetic field force on charged particles and for determining the velocity of the object.

Make sure to practice the right-hand rule for cross-product after reading this article.

Dot Product vs Cross Product

When studying technical subjects like physics or mathematics, one of the most common questions we find ourselves asking is, “Why should we study this and how is it going to help us in the future?”

I’d love to answer this question for you. The truth is, every aspect of the subjects you learn have some or the other application in your real-life, be it skill wise, content wise, or simply as a matter of gaining an attribute.

A common topic that every student would despise getting into, is vector algebra. Although it may look tricky at face value, in this article we’re going to cover the difference between cross product and dot product. Before we step into it, let’s understand what vector algebra is and how its study can be beneficial.

Vector algebra, as its name suggests, deals with vectors. Most quantities are either scalars or vectors. Scalars only have magnitude whereas vectors have both magnitude and direction.

Now that we’ve understood the importance of vector algebra, let’s get into dot product and cross product specifically.

Difference between cross product and dot product

1. The main attribute that separates both operations by definition is that a dot product is the product of the magnitude of vectors and the cosine of the angles between them whereas a cross product is the product of magnitude of vectors and the sine of the angles between them.

2. While this is the dictionary definition of what both operations mean, there’s one major characteristic that segregates them both. That difference can be noted in terms of vector algebra. The result of a dot product is a scalar quantity with magnitude as its whole, however, the result of a cross product is a vector quantity with both magnitude and direction.

These are the two main differences you must take note of to understand the concepts at face value.
Let’s take a mathematical approach to get familiar with it a bit more:

A dot product is represented the following way:

 a . b = ||a|| ||b|| cos (θ)

Here A and B are vectors and is the angle between both vectors.

A Cross product is represented the following way:

 a . b = ||a|| ||b|| sin (θ) n

Here A and B are vectors and is the angle between them. N is the unit vector perpendicular to the plane that A and B are a part of.

DOT PRODUCT VS CROSS PRODUCT (Tabular Form)

This will give you a summed up idea of the differences between both operations, in simpler words.

Factors of Comparison Dot Product Cross Product
General Definition Product of magnitude of vectors and cos of the angle between them.Product of magnitude of vectors and sine of the angle between them.
Mathematical Formula In terms of vectors A and B

A · Β = |A| |B| cos θ		In terms of vectors A and B

A × Β = |A| |B| sin θ n
Result The final product is a scalar quantity.The final product is a vector quantity
Result With further explanationScalar: Only Magnitude.Vector: Both magnitude and direction.
Property 1: Commutativity Follows a commutative law:
A.B=B.A		Does not follow a commutative law: AxB is not equal to BxA
Property 2: Orthogonality of vectors The dot product is zero when the vectors are orthogonal, as in the angle is equal to 90 degrees.
What can also be said is the following:

If the vectors are perpendicular to each other, their dot result is 0. As in, A.B=0		Whereas, the cross product is maximum when the vectors are orthogonal, as in the angle is equal to 90 degrees.
What can also be said is the following:

If the vectors are parallel to each other, their cross result is 0. As in, AxB=0
Property 3: Distribution Dot products distribute over addition Cross products also distribute over addition
Property 4: Scalar Multiplication LawScalar Multiplication Law is followed by Dot Products Scalar Multiplication Law is also followed by Cross Products

What does this mean theoretically?

 Dot Product :

Due to having only magnitude and no direction, both vectors in a dot product operation are aligned the same way. The cosine of the angle between these vectors is taken. The product comes out to be scalar. It is also known as inner product or projection product.
Dot productThe product has 4 distinct properties known as commutative, distributive, orthogonal, or one that follows the scalar multiplication law.

Applications of Dot Product:
The operation is used to define the length between two points on a plane, with known coordinates.

Cross Product :

Due to having both magnitude and direction, the magnitude of the vectors is taken along with the sine of the angle between them. As a result, the product comes out to be a vector quantity. It’s important to note that the final result of the cross product operation must be perpendicular to both vectors, or in other words, the plane that both vectors lie on.
cross product - crossproductcalculator.org

Thus, the right-hand thumb rule can be used to find the direction. In that case, the two fingers represent the vectors and the thumb determines the product. A cross product is also known as directed area product.

Just like the dot product, cross product also has 4 distinct properties. It is non-commutative, distributive, orthogonal, and compatible with the scalar multiplication law.

Applications of Cross Product:
Mainly applied in computational geometry to find or define the distance between two skew lines. Cross product can also be used to suggest if two vectors are coplanar or not.

dot product vs cross product

Conclusion:

Vector algebra that covers dot and cross products is a beneficial topic for aspiring physicians and mathematicians as it gives an insight into basic geometry and trigonometry that can be applied in real-world situations. In mathematics, addition, subtraction, and multiplication on vectors can be performed to understand the nature of a plan or trajectory, whereas in physics, vectors like distance, displacement, velocity, and acceleration are used to understand more extreme subjects.

Euclidean’s vectors have been used for several hundred years now, making a lot of contributions to the math and physics sectors. They were analyzed, evaluated, and reworked on after several scientists and mathematicians developed the concept, making alterations and innovations as new information would come into the picture.

Once understood, vectors can be an interesting topic to further your study on, and also apply in your life. We hope this article on dot and cross products helped you to understand the basic differences in terms of formula, properties, and applications!

Dot Product

Calculus is a complex part of Math. Even genius minds need to understand its core fundamentals to grasp this branch of arithmetic.

To calculate the position of anything that exists and has dimensions, cross product and dot product are used. These consider the coordinates of the number of dimensions, their magnitudes, and directions, finally giving the exact position.

This is done to define a particle’s address in the unlimited space around us. Let’s take, for instance, an electron.

It is so minute that you cannot calculate its location using centimeters or even millimeters. Also, it is inevitable to figure out the location without considering different dimensions because of its tininess.

Hence, Dot Product is what you need to get a pinpoint site of a nanoscopic particle.

What is a DOT PRODUCT?

With various directions and magnitudes, you need to consider when calculating the position of any particle/object in space (both two and three dimensions). Hence, these have been divided into two calculation types that will bifurcate separate calculations for easy understanding.

There are two lanes to go down; the first uses the cross product, whose product is again vector in nature. The second is using dot product, whose product is not a vector but a scalar.

Dot product

A scalar value is a number that gives a definite value, unlike a vector product that is not definite and is instead a variable. Although this difference is present, it does have the magnitude and direction of its product.

What is the Dot Product of Two Vectors?

Since its a product, it will involve two different values. So these are multiplied to get the final product.

Dot Product determines the similarity between the two selected values for calculation and not the difference between them like the cross product. Therefore, it can be both positive and negative in its value.

Let us consider two different vectors, a and b. The product between these two vectors, a and b, is called a ‘Dot Product.’

a . b = ||a|| ||b|| cos (θ)

  • a and b are the two vectors.          
  • θ is the angle between the two vectors a and b (ranges between 0° to 180°).

The angle between the two vectors is significant. This angle decides whether the dot product will be positive or negative (or bigger or smaller in value).

For example, let us consider two cases,
Case 1:
Let the θ value be ‘0’, meaning both the vectors overlap each other without the slightest discrepancy. They are perfectly aligned, pointing in the same direction.

So, the representation will become –  a . b = ||a|| ||b|| cos (0)

Cos (0) = 1

Therefore, whatever the value of a and b may be, now that the angle value is 1, the product between them will give the dot product a greater than 1.

The greater the dot product value, the similar will be the value of the direction of the particle/object in question.

Case 2:

Let the θ value be ‘1’, meaning both the vectors are perpendicular to each other precisely at right-angled positions. Thus, in the directional sense, if one points north, the other is pointing at east.

So, the representation will become –  a . b = ||a|| ||b|| cos (90)

Cos (90) = 0

Therefore, whatever the value of a and b may be, now that the angle value is 0, the product between them will be obviously 0.

Case 3:
How can a dot product be negative?
If the angle between them is cos (180), i.e., both the vectors are connected by one of their ends, pointing in opposite directions, then the value will indeed be 1, but with a negative sign before it. And so, the negative existence of dot product can be justified.

Dot Product Formula

There are two formulae, depending on the type of mode of calculation. The value will remain the same for both types, except for representation.

Algebraic Expression

A concise expression has been formulated for easy calculation. And that is –

Where, a is first vector
b is second vector
Σ is summation; it is the total of all the dimensional dot product values
n is the dimension number (n=1,2,3,……..)

Here, a1, a2, a3………an are all the values only concerning vector a, but in different dimensions, like

a1 is for x-axis,
a2 is for y-axis
a3 is for z-axis
And so on.
The same is the case for vector b.
Values of both a and b vectors are used to get the final product.

Geometric Expression

This expression, unlike the Algebraic Expression, involves the angle. Hence, θ holds much importance here.

The Geometric Expression is –  a . b = ||a|| ||b|| cos (θ)

Where, a and b are the two vectors.
θ is the angle between the two vectors, a and b.

Here, θ are mostly 0°,30°, 45°, and 90°, and their respective values are 1, √3/2, √1, and 1/2.

How to do Dot product?

To do Dot Product, there are two methods in Algebraic Expression. However, there can be more than two methods if there are more than two dimensions: three or four and so forth.

Two-Dimensional Dot Product :

The Algebraic Expression for a two-dimensional representation is –
a · b = ax × bx + ay × by

Where, a and b are the two vectors of which the dot product is to be calculated.

ax is the x-axis
ay is the y-axis

are the values of the vector a.

bx is the x-axis
by is the y-axis

are all the values of the vector b.

On solving the above expression, you will get the dot product of a two-dimensional particle/object.

Three-Dimensional Dot Product :

The Algebraic Expression for a three-dimensional representation is almost the same; save the addition of another dimension after x and y, i.e., z.

a · b = ax × bx + ay × by + az × bz

Where, a and b are the two vectors of which the dot product is to be calculated.

ax is the x-axis
ay is the y-axis
az is the z-axis

are all the values of the vector a.

bx is the x-axis
by is the y-axis
bz is the z-axis

are all the values of the vector b.

On solving the above expression, you will get the dot product of a three-dimensional particle/object.

Dot product Examples

Algebraic Expression

Two-Dimensional Dot Product

E.g. The coordinates for the x-axis and y-axis for the vectors a and b are given as (-4,8) and (3,6)

Solution: Substitute the coordinate values in the formula for the two-dimensional dot product.

Formula : a · b = ax × bx + ay × by

Substituting, we get –

a . b = (-6 × 5) + (8 × 12)

On solving, we get –

a . b = (-30) + (96)
a . b = -30 + 96
a . b = 66

Therefore, the dot product of vectors a and b is 66.

Three-Dimensional Dot Product

E.g. The coordinates for the x-axis, y-axis, and z-axis for the vectors a and b are given as – (4,8,10) and (9,2,7)

Solution: Substitute the coordinate values in the formula for the two-dimensional dot product.

Formula – a · b = ax × bx + ay × by + az × bz

Substituting, we get –

a . b = (4 × 9) + (8 × 2) + (10 × 7)

On solving, we get –

a . b = (36) + (16) + (70)
a . b = 36 + 16 + 70
a . b = 122

Therefore, the dot product of vectors a and b is 122.

Geometric Expression

E.g.  For vectors a and b, the values are 10 and 13. The value of θ is 59.5°

Solution: Substitute the values in the formula.

Formula – a . b = ||a|| ||b|| cos (θ)

Substituting, we get –

a . b = ||10|| ||13|| cos (59.5)

On solving, we get –

a . b = ||10|| ||13|| 0.5075
a . b = 10 × 13 × 0.5075
a . b = 65.98 which is almost 66

Therefore, the dot product of vectors a and b is 66. Now go back and compare the answer we got using Algebraic Expression.

You will observe that both the answers are ‘66’ irrespective of the method used. Hence it is proved that both the methods result in the same.

Conclusion

On a moderate level, the dot product is used in math and physics. On a larger scale, the dot product is used to study space, its components, what type of particles and objects are found, their dimensions, etc.

Therefore, the dot product is essential and significant for discovering the still hidden secrets of space.

Dot Product